Nutbuster
by Mark Nauseef

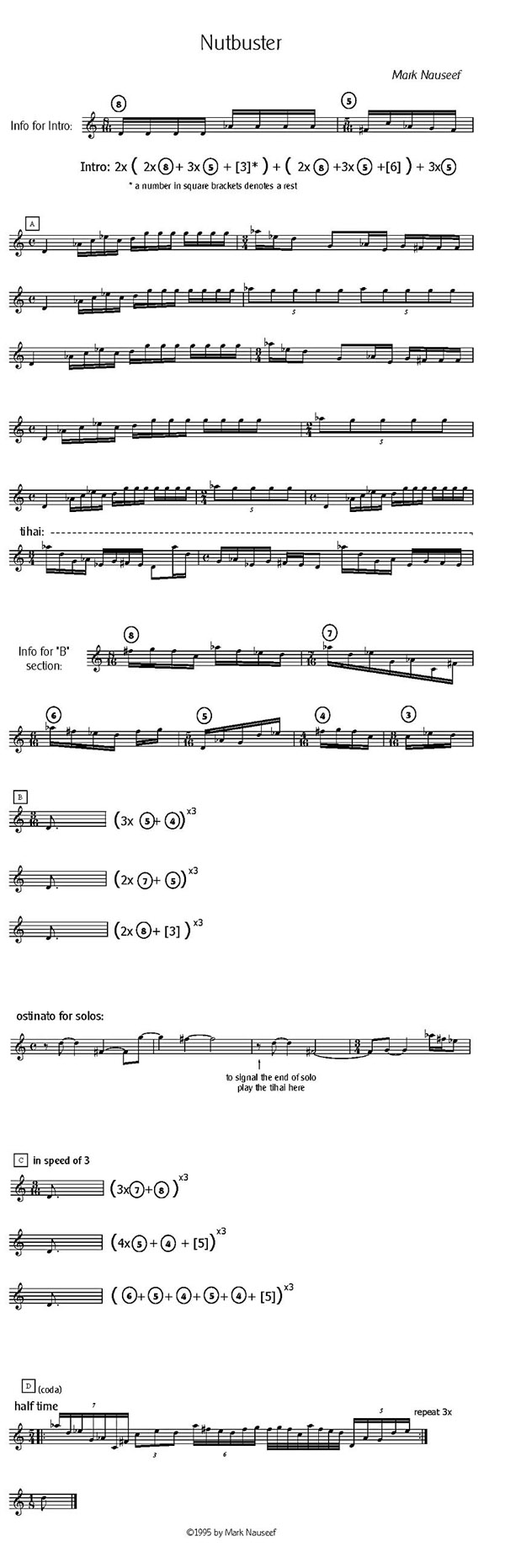
(see the score at the bottom of text)

Nutbuster utilizes concepts such as sub-division, cycles, reduction and phrasing / grouping in various “speeds per pulse”. The purpose of this article is to look at ways of using these concepts with a limited amount of melodic material which is made into modules of different sizes that can be stretched, squashed, sped-up and slowed down while keeping a constant pulse. These concepts can be heard at the highest levels of execution in Indian music where these ideas are used to build long and complex structures filled with mathematical calculations and illusion. The simple examples of these concepts used in Nutbuster were “borrowed” from Indian classical music, with the greatest respect.

Melodically, this piece is based on a group of six notes (C, D, Eb, F#, G, Ab). As the piece only uses those notes, and groups them into recurring modules, parts of Nutbuster have been written as a formula / equation. Writing with formulas containing modules can be useful when composing pieces that include permutation or repeating of the same material. Not only does it reduce the number of pages needed to produce the chart / score, but also becomes a good exercise for the player, as the most effective way in playing the piece is through memorization.

As the piece is under three minutes in duration, there is no time for the long development that happens in Indian music. The use of these Indian rhythmic mechanisms in Nutbuster is basic but gives an idea of how such concepts can be used in putting pieces together.

The “Info for Intro” and the “Info for B section” should be memorized.

The Elements

- Cycles – The intro, sections A, B, C and the ostinato are all in fifteen beat / pulse cycles. The D section is also in a fifteen beat / pulse cycle but “felt” and played in half time. In western terms, the quarter note pulse becomes a half note pulse during section D.

Points of interest concerning cycles

Section A - By keeping track of the 15/4 pulse through some means of physical time reference, such as keeping tal, a conducting pattern, stepping, etc., it is possible to perceive the same phrase in various ways as the reduction of the material places the “one” of the phrase in a different relationship to the pulse, each time the phrase repeats.

Sections B and C - Each equation is repeated three times in order to fill the space of the fifteen pulse / beat cycle(s) (one cycle for Section B and two cycles for letter C). As mentioned before, by keeping a form of physical time reference, such as keeping tal, conducting, clapping, stepping, etc., it is possible to feel the same phrase in different parts of the beat / pulse as it is repeated within the cycle(s). By keeping a two beat physical time pattern such as stepping RLRL…etc. clapping-waving or keeping a backbeat (as in the recording) it is possible to feel the same phrase have a completely different feeling as it crosses over the “two” rhythm or backbeat.

- Reduction – In section A (bars 1 - 11), a reduction is caused by eliminating phrases each time that the material returns to the low D to repeat the phrase first played in bars 1 - 4. So, in bars 5 – 8, the material from bars 1 – 4 is repeated but drops or eliminates the last quintuplet. In the next two bars more material is eliminated, reducing the melodic line and leaving only the first bar of the A section (bar 11). Of course it is also possible to go the other way and build a composition through gradual expansion.

- Sub-division and Speeds Per Pulse – Sections B and C are built on the concepts of sub-division and speeds per pulse. Sub division is shown by the numbers used in the equations in both of these sections. The speed or rate per pulse in section B is four beats per pulse. This means that the sixteenth notes which make up the cycle of fifteen large pulses and would “normally” be written in groups of four (if each pulse equals one quarter note this would be four sixteenth notes per quarter note) are sub-divided into groups of 5/16, 4/16, 7/16, 8/16, 3/16 (this includes sounded (played) and unsounded (rests) notes or beats.

There is also sub-division in section C. The sub –divisions used in section C are played at the speed per pulse of three or triplet time. It is very important that the player feels comfortable phrasing in groupings of seven, five and eight beats while playing in the speed of three (triplets). This is the essence. To phrase with any grouping possible, while feeling a “speed per pulse”. In this simple example in section C, these small phrases have a different feeling and sound, as they permutate across the pulse. This concept can get very serious and there is no better example than Indian musicians. Through permutation and combination of small phrases being played in various speeds per pulse, there are enormous possibilities for building compositions. As little as one five-note phrase when played in various speeds per pulse can be a wealth of information.

Also “borrowed” from Indian music, is the Tihai. A tihai is a rhythmic cadence containing a phrase which is repeated three times so that it finishes / resolves on the downbeat or “one” of the next material. There are exceptions to this in Indian music, where the resolution is not on the “one”, but the use of the tihai in Nutbuster, resolves directly on the “one”. This simple form of tihai takes place during the last three bars of section A. (bars 12, 13, 14 of section A). It is also used as a signal from the soloist, to move to Section B. This happens on the ninth beat of the fifteen beat cycle (at bar three of the ostinato).

Although this is a simple example of a tihai, it is possible to see how the phrase that is repeated three times is perfectly symmetrical in the way it works across the pulse. As mentioned before, keeping a “physical time reference” of “downbeat” while reciting or playing, will allow the player to feel the sensation of independence as the phrase which is repeated three times switches between an downbeat and upbeat feeling.

Summary

- Rhythmic modules (with or without specific pitches)

- Cycles

- Sub-division

- Speeds per pulse

- Permutation / Combination

- Reduction / Expansion

You can hear a good version of "Nutbuster" on "The Old Country"

Here's the score (or download a printable Adobe Acrobat pdf file here):

back